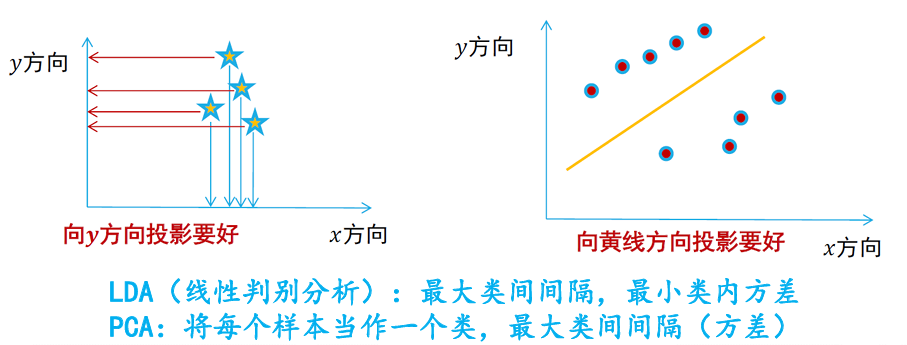
04 无监督学习
01 K-means
- 若干定义:
- n 个 m-维数据
, (1≤i≤n) - 两个 m 维数据之间的欧氏距离为
值越小,表示 和 越相似;反之越不相似
- n 个 m-维数据
- 聚类集合数目 k
- 问题: 如何将 n 个数据依据其相似度大小将它们分别聚类到 k 个集合,使得每个数据仅属于一个聚类集合。
算法流程
- 初始化聚类质心
- 初始化
个聚类质心 - 每个聚类质心
所在集合记为
- 初始化
- 将每个待聚类的数据放入唯一一个聚类集合中
- 计算待聚类数据
和质心 之间的欧氏距离 - 将每个
放入与之距离最近聚类质心所在聚类集合中,即
- 计算待聚类数据
- 更新聚类质心
- 根据每个聚类集合中所包含的数据,更新该聚类集合质心值,即:
- 根据每个聚类集合中所包含的数据,更新该聚类集合质心值,即:
- 算法迭代,直至满足条件
- 迭代次数上限
- 质心基本不变
欧式距离,也可以换成方差
- 最小化簇内距离,最大化簇间距离
不足:
- 欧氏距离假设数据每个维度之间的重要性是一样的
- 需要初始化聚类质心,初始化聚类中心对聚类结果有较大的影响
- 需要事先确定聚类数目,很多时候我们并不知道数据应被聚类的数目
K-medoids Algorithm
Chooses input data points as centers;
选择输入的数据点作为聚类中心
Works with an arbitrary matrix of distances between data points instead of Euclidean distance
可以用别的距离度量公式
02 主成分分析
主成分分析是一种特征降维方法
概念解析
- 方差
- 对象:n 个数据
- 方差等于各个数据与样本均值之差的平方和之平均数
- 方差描述了样本数据的波动程度
- 对象:n 个数据
- 协方差
- 对象:n 个 2 维变量数据
- 衡量两个变量之间的相关度
- 对象:n 个 2 维变量数据
- Pearson Correlation coefficient
- 将两组变量的关联度规整到一定的范围内
- 性质:
的充要条件是存在常数 和 , 使得 - 皮尔逊相关系数是对称的,即 corr
- 作用:刻画两个变量之间的线性相关度
- 如果
的取值越大,则两者在线性相关的意义下相关程度越大。 表示两者不存在线性相关关系 (可能存在其他非线性相关的关系)。
- 如果
- 将两组变量的关联度规整到一定的范围内
- 相关性 correlation 与独立性 independence
- 如果 X 和 Y 的线性不相关,则
- 如果
和 的彼此独立,则一定 , 且 和 Y 不存在任何线性或非线性关系 - “不相关” 比 “独立” 弱
- 如果 X 和 Y 的线性不相关,则
算法动机
主成分分析:特征降维的方法,但要保证降维后的结果要保持原始数据固有结构
- 需要尽可能将数据向方差最大方向进行投影,使得数据所蕴含信息没有丢失,彰显个性
- 将𝒅维特征数据映射到𝒍维空间(𝒅≫𝒍),去除原始数据之间的冗余性(通过去除相关性手段达到这一目的)
- 将原始数据向这些数据方差最大的方向进行投影。一旦发现了方差最大的投影方向,则继续寻找保持方差第二的方向且进行投影(保证方向的正交性)
| 线性判别分析 | 主成分分析 | |
|---|---|---|
| 是否需要样本标签 | 监督学习 | 无监督学习 |
| 降维方法 | 优化寻找特征向量 |
优化寻找特征向量 |
| 目标 | 类内方差小、类间距离大 | 寻找投影后数据之间方差最大的投影方向 |
| 维度 | LDA 降维后所得到维度是与数据样本的类别个数 |
PCA 对高维数据降维后的维数是与原始数据特征维度相关 |
算法描述
假定每一维度的特征均值均为零(已经标准化)
降维后 n 个 l 维样本数据 Y 的方差为:
降维前 n 个 d 维样本数据 X 的协方差矩阵记为:
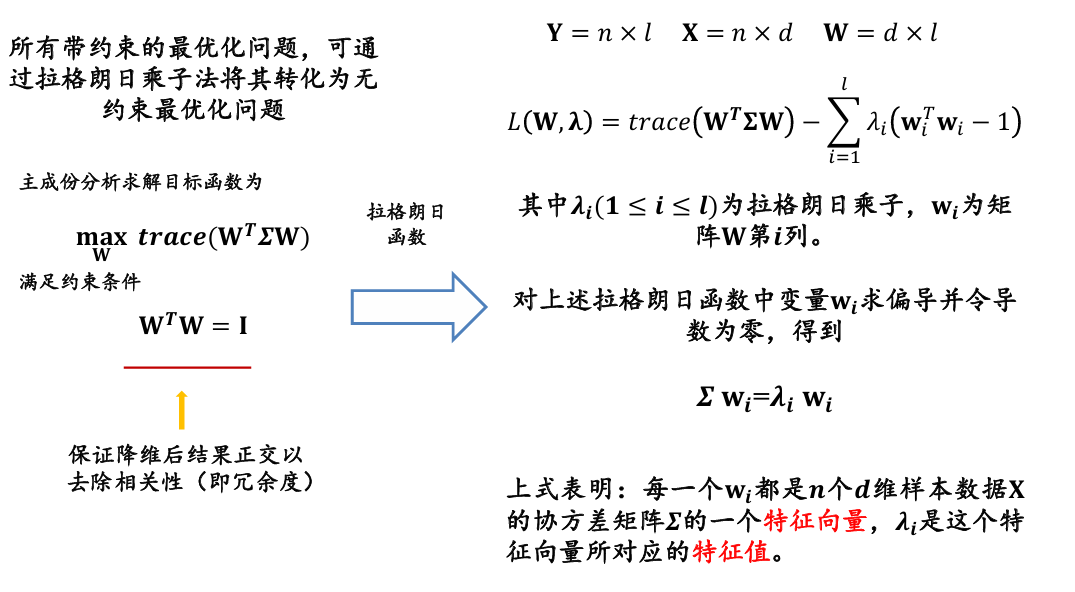
主成份分析的求解目标函数为
满足约束条件
保证降维后结果正交以去除相关性(即冗余度)
- 在主成份分析中,最优化的方差等于原始样本数据 𝐗 的协方差矩阵 𝜮 的特征根之和
- 要使方差最大,我们可以求得协方差矩阵 𝜮 的特征向量和特征根,然后取前 𝒍 个最大特征根所对应的特征向量组成映射矩阵 𝐖 即可
- 输入:n 个 d 维样本数据所构成的矩阵 X,降维后的维数为 l
- 输出:映射矩阵
- 对于每个样本数据
进行中心化处理: - 计算原始样本数据的协方差矩阵:
- 对协方差矩阵
进行特征值分解,对所得特征根按其值大到小排序 - 取前
个最大特征根所对应特征向量 组成映射矩阵 W - 将每个样本数据
按照如下方法降维:
其他降维方法
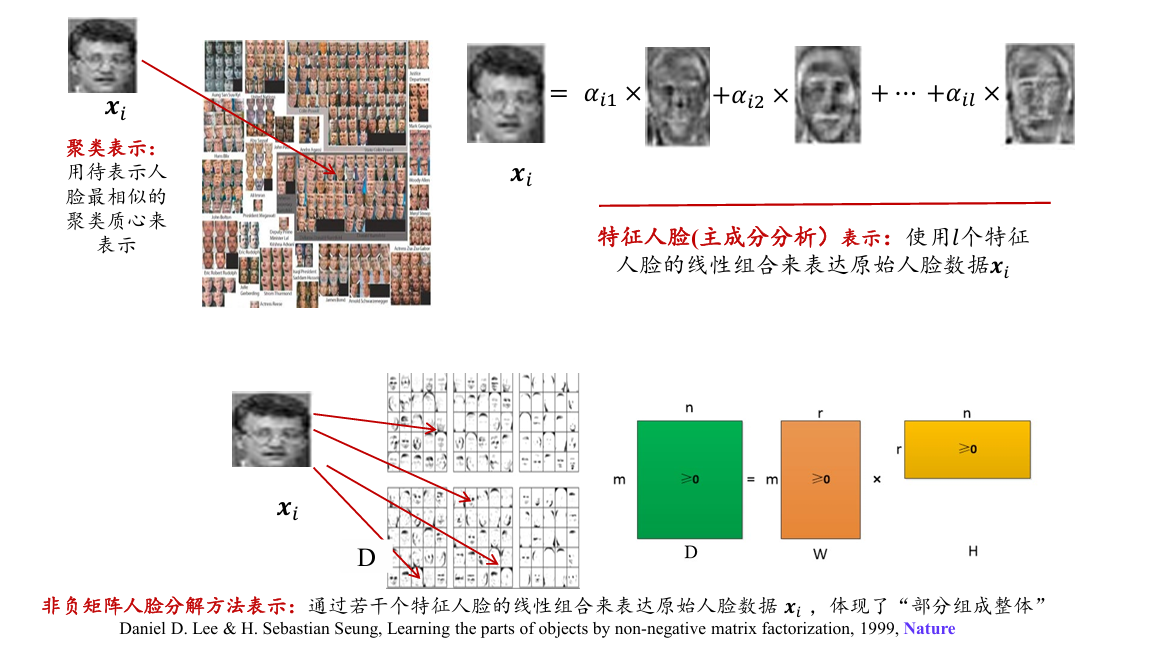
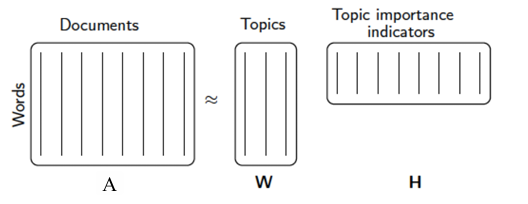
- 非负矩阵分解(non-negative matrix factorization, NMF)
- 将非负的大矩阵分解成两个非负的小矩阵
- 多维尺度法(Metric multidimensional scaling, MDS)
- 局部线性嵌入(Locally Linear Embedding,LLE)
非负矩阵分解 PCA
非负矩阵分解将给定的非负矩阵
- 其中,
, 。 - 代价函数:度量原始矩阵 𝐷 与其近似矩阵 𝑊𝐻 之间的误差
- 欧氏距离函数
- KL 散度函数
多维尺度法 MDS
保持原始数据之间两两距离不变:MDS 算法会计算原始数据两两之间的距离,形成一个距离矩阵,以此来保证降维之前距离近的数据在降维之后也能很接近
无法对新数据集合进行降维(比如测试集),因为需要先验的距离矩阵知识
令 N 是原始数据数量, 每个数据由 d 维特征表示, 即
- 可以将所有原始数据表示为
,
多维尺度法首先计算任意两个数据
- A 是一个
大小的矩阵, 和 之间的距离度量函数由具体应用来定 (如可选取余弦距离等)
接着计算中心化矩阵
假设矩阵 B 的秩为 p,对矩阵 B 进行奇异值分解,可得:
是一个对角矩阵,对角线上的元素为矩阵 B 的非零特征根 是一个 n×l 矩阵,其中 为特征根 所对应的特征向量
于是
其中
局部线性嵌入 LLE
PCA 和 MDS 都属于线性降维方法,LLE 是一种非线性降维方法
假设数据是局部线性的 (即使数据的原始高维空间是非线性流形嵌入),这时可以用和邻居数据的线性关系进行局部重构
- 保持邻域内的线性关系,并使得该线性关系在降维后的空间中继续保持
03 特征人脸方法
用(特征)人脸表示人脸,而非用像素点表示人脸
将每幅人脸图像转换成列向量
- 如将一幅 32 × 32 的人脸图像转成 1024 × 1 的列向量
输入:
输出:映射矩阵 W
算法步骤:
- 对于每个人脸样本数据
进行中心化处理: - 计算原始人脸样本数据的协方差矩阵:
用代替大的协方差矩阵计算,避免 d 维度过高计算复杂 - 对协方差矩阵
进行特征值分解,对所得特征根从到小排序 - 取前
个最大特征根所对应特征向量 组成映射矩阵 W - 将每个人脸图像
按照如下方法降维:
04 潜在语义分析
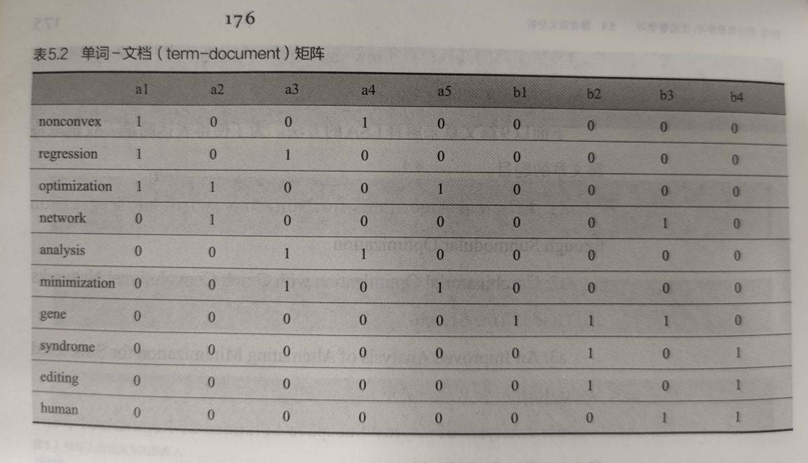
潜在语义分析先构建一个单词-文档 (term-document) 矩阵 A,进而寻找该矩阵的低秩逼近 (low rank approximation),来挖掘单词-单词、单词-文档以及文档-文档之间的关联关系
第一步,计算单词-文档矩阵:
第二步,奇异值分解:
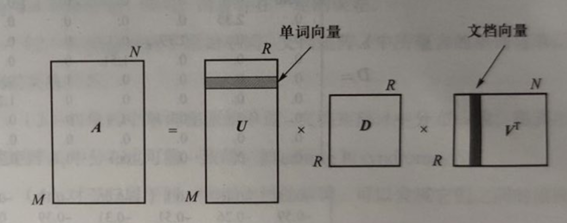

第三步,重建矩阵:
- 当 k=2, 即选取最大的前两个特征根及其对应的特征向量对矩阵 A 进行重建。下面给出了选取矩阵 U、矩阵 D 和矩阵 V 的子部分重建所得矩阵
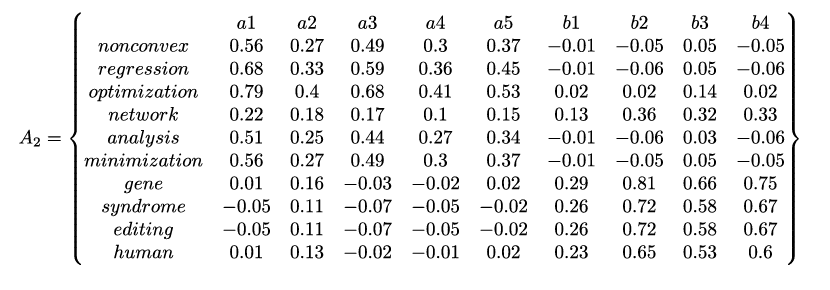
第四步,挖掘语义关系:
- 基于单词-文档矩阵 A,可以计算任意两个文档之间的皮尔逊相关系数,从而得到如下文档-文档相关系数矩阵:
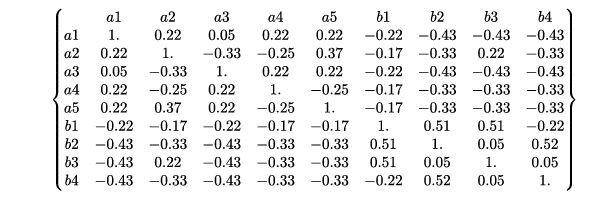
- 基于重建单词-文档矩阵 A 2,可以计算任意两个文档之间的皮尔逊相关系数,从而得到如下文档-文档相关系数矩阵:
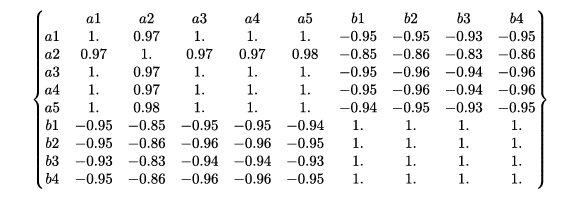
Conclusion:
- 基于重建单词-文档矩阵 𝐴2 得到的相关系数矩阵中文档-文档之间的相关关系更加明确
- 在同一文档中出现过的单词之间相关系数趋近为 1,没有同时出现在同一文档中的单词之间相关系数趋近为-1
05 期望最大化算法
无论是最大似然估计算法或者是最大后验估计算法,都是充分利用已有数据,在参数模型确定 (只是参数值未知) 情况下,对所优化目标中的参数求导,令导数为 0,求取模型的参数值
在解决一些具体问题时,难以事先就将模型确定下来
期望最大化(expectationmaximization, EM)
- 解决含有隐变量 (latent variable) 问题的参数估计方法
- 算法分为两个步骤:
- 求取期望(E 步骤,expectation)
先假设模型参数的初始值,估计隐变量取值 - 期望最大化(M 步骤, maximization)
基于观测数据、模型参数和隐变量取值一起来最大化“拟合”数据,更新模型参数 - 然后,基于所更新的模型参数,得到新的隐变量取值 (E 步骤),然后更新参数 (M 步骤), 直至算法收敛
- 求取期望(E 步骤,expectation)
二硬币投掷
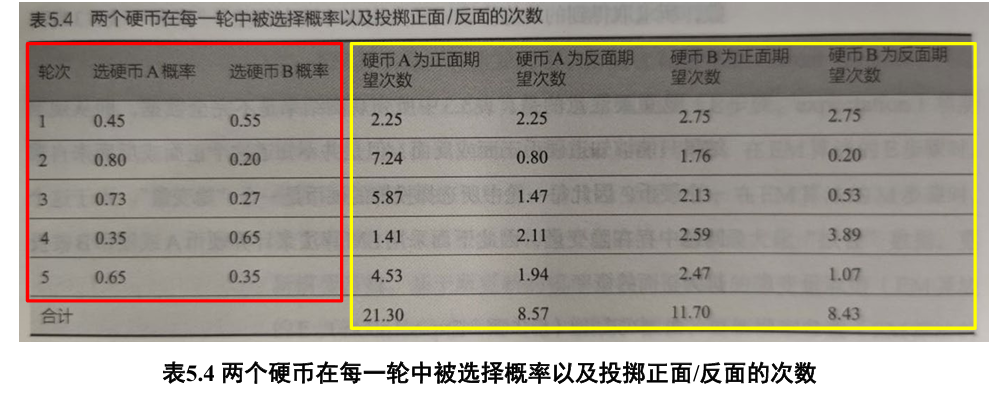
假设有 A 和 B 两个硬币,进行五轮掷币实验
- 每一轮实验中,先随机选择一个硬币,然后用所选择的硬币投掷十次,将投掷结果作为本轮实验观测结果
- H 代表硬币正面朝上、T 代表硬币反面朝上
实验结果如下:

问题:从这五轮观测数据出发,计算硬币 A 或硬币 B 被投掷为正面的概率; 记硬币 A 或硬币 B 被投掷为正面的概率为
| 问题分析 | |
|---|---|
| 隐变量 | 每一轮选择硬币 A 还是选择硬币 B 来完成 10 次投掷 (选择硬币 A 或硬币 B 投掷的概率) |
| 模型参数 | 硬币 A 和硬币 B 投掷结果为正面的概率 |
E 步骤
估计隐变量取值: 选择硬币 A 或硬币 B 的投掷概率
假设
由 B 所得概率为:
对每一轮计算:
- 例如,第一轮中硬币 A 正面的期望次数 =
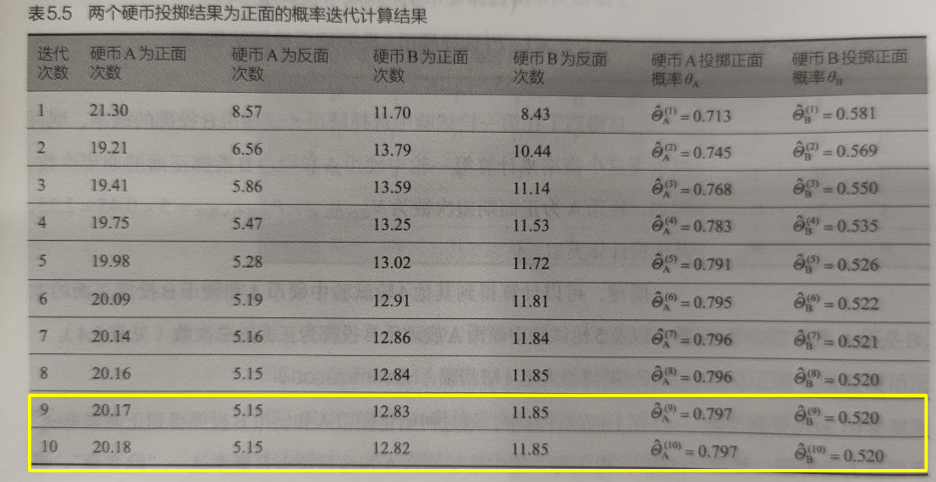
M 步骤
在 E 步骤的信息基础上,可更新得到硬币 A 和硬币 B 投掷为正面的概率:
可在新的概率值
三硬币投掷
假设有三枚质地材料不均匀的硬币 (每枚硬币投掷出现正反两面的概率不一定相等) 这三枚硬币分别被标记为 0,1,2
- 约定出现正面记为 H,出现反面记为 T
一次试验的过程如下:
- 首先掷硬币 0
- 如果硬币 0 投掷结果为 H,则选择硬币 1 投掷三次
- 如果硬币 0 投掷结果为 T,则选择硬币 2 投掷三次
- 观测结果中仅记录硬币 1 和硬币 2 的投掷结果,不出现硬币 0 的投掷结果
- 因为硬币 0 的投掷结果没有被记录,所以是未观测到的数据 (隐变量)
对问题进行如下建模:
- 未观测数据取值集合记为
- 观测数据取值集合记为
- 模型参数集合 (三枚硬币分别出现正面的概率) 为
- 在 n 次试验中,未观测到的数据序列记为 z,观测到的数据序列记为 x,观测到的数据序列中有 h 次为正面朝上, t 次反面朝上
通过贝叶斯公式,可以从观测数据来推测未观测数据的概率分布,即从硬币正面和反面观测结果来推测硬币 0 投掷为正面或反面这一隐变量:
随后的算法操作跟二硬币投掷是一致的,不再赘述
