07 人工智能博弈
01 相关概念
定义
- 参与者或玩家(player):参与博弈的决策主体
- 策略(strategy):参与者可以采取的行动方案,是一整套在采取行动之前就已经准备好的完整方案。
- 某个参与者可采纳策略的全体组合形成了策略集(strategy set)
- 所有参与者各自采取行动后形成的状态被称为局势(outcome)
- 如果参与者可以通过一定概率分布来选择若干个不同的策略,这样的策略称为混合策略 (mixed strategy)。若参与者每次行动都选择某个确定的策略,这样的策略称为纯策略 (pure strategy)
- 收益(payoff):各个参与者在不同局势下得到的利益
- 混合策略意义下的收益应为期望收益(expected payoff)
- 规则(rule):对参与者行动的先后顺序、参与者获得信息多少等内容的规定
研究范式:建模者对参与者(player)规定可采取的策略集 (strategy sets) 和取得的收益,观察当参与者选择若干策略以最大化其收益时会产生什么结果

博弈的分类
- 合作博弈与非合作博弈
- 合作博弈(cooperativegame):部分参与者可以组成联盟以获得更大的收益
- 非合作博弈(non-cooperative game):参与者在决策中都彼此独立,不事先达成合作意向
- 静态博弈与动态博弈
- 静态博弈(static game):所有参与者同时决策,或参与者互相不知道对方的决策
- 动态博弈(dynamic game):参与者所采取行为的先后顺序由规则决定,且后行动者知道先行动者所采取的行为
- 完全信息博弈与不完全信息博弈
- 完全信息(complete information):所有参与者均了解其他参与者的策略集、收益等信息
- 不完全信息(incompleteinformation):并非所有参与者均掌握了所有信息
博弈的稳定局势 👉 纳什均衡:如果在一个策略组合上,当所有其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡
- Nash 定理:若参与者有限,每位参与者的策略集有限,收益函数为实值函数,则博弈必存在混合策略意义下的纳什均衡
- 囚徒困境中两人同时认罪就是这一问题的纳什均衡



- 归纳法证明即可
02 博弈策略求解
遗憾最小化算法
对于一个有 N 个玩家参加的博弈,玩家 i 在博弈中采取的策略记为
- 对于所有玩家来说,他们的所有策略构成了一个策略组合,记作
- 策略组中, 除玩家 i 外,其他玩家的策略组合记作
最优反应策略:
- 给定策略组合
, 玩家 在终结局势下的收益记作 - 在给定其他玩家的策略组合
的情况下,对玩家 i 而言的最优反应策略 满足如下条件: 是玩家 可以选择的所有策略
在策略组合
在有限对手、有限策略情况下,纳什均衡一定存在
此时,策略组
算法定义
遗憾最小化算法是一种根据以往博弈过程中所得遗憾程度来选择未来行为的方法
玩家 i 在过去 T 轮中采取策略
其中
简单地说,累加遗憾值代表着在过去 T 轮中,玩家 i 在每一轮中选择策略
遗憾匹配:
- 获取玩家 𝑖 的所有可选策略的遗憾值
- 根据遗憾值的大小来选择后续第 𝑇+1 轮博弈的策略
定义有效遗憾值:遗憾值为负数的策略 👉 不能提升下一时刻收益
利用有效遗憾值的遗憾匹配可得到玩家
表示玩家 所有策略的总数
依照一定的概率选择行动是为了防止对手发现自己所采取的策略(如采取遗憾值最大的策略)
问题描述:假设两个玩家 A 和 B 进行石头-剪刀-布(Rock-Paper-Scissors,RPS)的游戏,获胜玩家收益为 1 分,失败玩家收益为-1 分,平局则两个玩家收益均为零分
第一局时,若玩家 A 出石头(R),玩家 B 出布(P),则此时玩家 A 的收益
- 对于玩家 A ,在玩家 B 出布(P)这个策略情况下,如果玩家 A 选择出布(P)或者剪刀(S),则玩家 A 对应的收益值
或者 - 即 T = 1 时
- 布策略遗憾值:
- 剪刀策略遗憾值:
- 布策略遗憾值:
- 即 T = 1 时
- 对于玩家 B,在玩家 A 出石头 (R) 这个策略情况下
- 即 T = 1 时
- 石头策略遗憾值:
- 剪刀策略遗憾值:
- 石头策略遗憾值:
- 即 T = 1 时
在第二局中:
- 玩家 A 选择石头、剪刀和布这三个策略的概率分别为 0、2/3、1/3
- 玩家 B 的有效遗憾值积累小于 0,所以随机选择策略
假设玩家 A 在第二局按照遗憾值最大的策略选择“剪刀”、玩家 B 随机选择“石头”,计算得到玩家 A 的累加遗憾值:
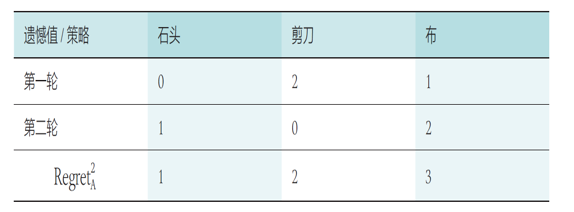
在第三局时,玩家 A 选择“石头”、“剪刀”和“布”的概率分别为 1/6 、 2/6(1/3)、 3/6(1/2)。
需要注意的是,玩家 A 既可以按照遗憾值最小在第三轮来选择“布”这一策略,又可以随机选择“石头”或“剪刀”以防止自己的策略被对手察觉
虚拟遗憾最小化算法
很多博弈(围棋、扑克)需要多次决策才能判断胜负,会导致博弈状态空间呈指数增长时,对一个规模巨大的博弈树无法采用最小遗憾算法,因此需要采取虚拟遗憾最小化算法(counterfactual regret minimization)
也就是说,一轮代表着多次决策,多次决策才能达到终局
算法理论
对于任何序贯决策的博弈对抗,可将博弈过程表示成一棵博弈树
- 每一个中间节点都是一个信息集 I,包含博弈中当前的状态
- 给定博弈树的一个节点,可以从一系列的动作中选择一个,然后状态发生转换,如此周而复始,直到终局(博弈树的叶子节点)
- 玩家在当前状态下可采取的策略就是当前状态下所有可能动作的一个概率分布
具体而言,在信息集 I 下,玩家可以采取的行动集合记作
- 玩家 i 所采取的行动
可认为是其采取的策略 的一部分 - 在信息集 I 下采取行动 a 所代表的策略记为
- 计算虚拟遗憾值的对象:每个中间节点在信息集下所采取的行动
- 然后根据遗憾值匹配,得到该节点在信息集下应该采取的策略
- 然后根据遗憾值匹配,得到该节点在信息集下应该采取的策略
在一次博弈中,所有玩家交替采取的行动序列记为
在策略组合
博弈的终结局势集合也就是博弈树中叶子节点的集合,记为
- 对于任意一个终结局势
,玩家 在此终点局势下的收益记作 - 给定行动序列
,依照策略组合 最终到达终结局势 的概率记作
在策略组合 σ 下,对玩家 i 而言,如下计算从根节点到当前节点的行动序列路径 h 的虚拟价值:
行动序列路径
- 经过路径 h 到达当前节点的概率 (仅考虑其他玩家策略)
- 从当前节点走到叶子结点(博弈结束)的概率 👉 终局情况
- 所到达叶子节点的收益 👉 终局收益
在定义了行动序列路径
- 当一个策略确定在信息集 I 上采取行动 a 时,就可能对"到达当前节点概率"以及"当前节点到叶子节点概率"产生影响
对能够到达同一个信息集
类似于遗憾最小化算法,虚拟遗憾最小化算法的遗憾值是
表示玩家 在第 轮中于当前节点选择行动 的遗憾值
进一步可以定义有效虚拟遗憾值:
根据有效虚拟遗憾值进行遗憾匹配以计算经过 T 轮博弈后,玩家 i 在信息集 I 情况下于后续 T + 1 轮选择行动 a 的概率:
问题描述:
- 两名玩家进行游戏博弈
- 游戏中仅提供牌值为 1、2 和 3 的三张纸牌
- 每轮中每位玩家各持一张纸牌,每位玩家根据各自的判断决定是否追加定额赌注
- 摊牌阶段比较未弃牌玩家的底牌大小,底牌值最大的玩家即为胜者
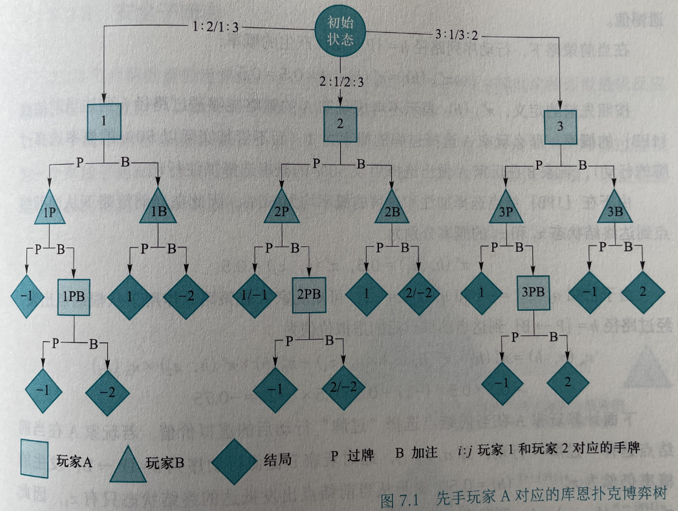
初始根结点下,三条边分别代表玩家 A 拿到三张不同手牌的情况
库恩扑克的信息集(即博弈树的中间结点)有 12 个:
在信息集中, P 表示过牌、B 表示下注
这里以信息集 {1PB} 为例, 来计算玩家 A 通过路径 1 → 1P → 1PB 到达当前节点 {1PB} 后选择“过牌”行动的遗憾值
- 在当前策略下, 行动序列路径 h = {P → B} 产生的概率:
玩家 B 在玩家 A 做出选择后以 50% 概率选择加注行动
- 当前策略下从当前节点到达终结状态
和 的概率分别为:
{1PB} 节点选择加注和过牌的概率均为 50%
- 可知玩家 A 在策略 σ 作用下从根节点出发、经过路径 h = {P → B} 到达当前节点后的虚拟价值:
已知
下面计算玩家 A 在当前节点选择“过牌”行动后的虚拟价值
- 若玩家 A 在当前节点选择“过牌”行动,即
,此时玩家 B 促使行动序列 发生的概率仍然为 - 由于从当前节点出发抵达的终结状态只有
,所以
则玩家 A 在当前节点选择“过牌”行动后的虚拟价值为:
最终,在信息集
在第一轮博弈中,累加虚拟遗憾值与行为遗憾值相同:
类似的,可以计算信息集
于是,根据遗憾值匹配算法计算结果,在下一轮的策略中会选择“过牌”策略
安全子博弈
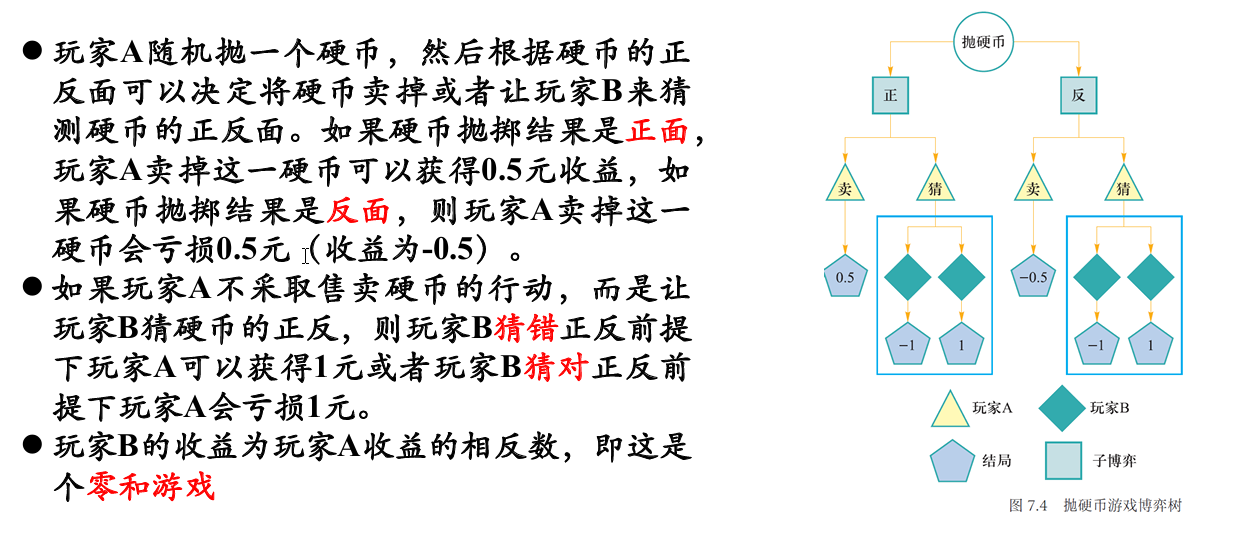
对于一个非完全信息的博弈,通常可以找到一些从全局出发的近似解法,例如使用上一节中的虚拟遗憾值最小化算法,所谓安全子博弈是指在子博弈的求解过程中,得到的结果一定不差于全局的近似解法
在上面抛硬币的例子当中,在猜硬币的过程中,如果玩家 B 的行动是通过预测玩家 A 卖掉硬币的收益来决定,猜硬币这个子博弈就是安全的。反之如果玩家 B 的行动仅考虑猜硬币的过程(本例中为不考虑 A 买硬币的收益),则猜硬币这个子博弈就是不安全的
03 博弈规则设计
如何设计博弈的规则,使得博弈的最终局势能尽可能达到整体利益的最大化
双边匹配问题: 稳定婚姻问题
在给定成员偏好顺序的情况下,为两组成员寻找稳定的匹配
假设有
他们有着如下偏好:
- 对于任意一名单身男性
, 都有自己爱慕的单身女性的顺序 ,
表示第 名男性所喜欢单身女性中,排在第 位的单身女性 - 对于任意一名单身女性
也有其爱慕的单身男性顺序
表示第 名女性所喜欢单身男性中,排在第 位的单身男性 - 算法的最终目标是为这
个男士和女士匹配得到 对伴侣,每一对伴侣可以表示为
不稳定匹配:对于两对潜在的匹配伴侣
稳定匹配问题的稳定解:不存在未达成匹配的两个人都更倾向于选择对方而不是自己当前的匹配对象
- 单身男性向最喜欢的女性表白
- 所有收到表白的女性从向其表白男性中选择最喜欢的男性,暂时匹配
- 未匹配的男性继续向没有拒绝过他的女性表白。收到表白的女性如果没有完成匹配,则从这一批表白者中选择最喜欢的男性
- 即使收到表白的女性已经完成匹配,但是如果她认为有她更喜欢的男性,则可以拒绝之前的匹配者,重新匹配
- 如此循环迭代,直到所有人都成功匹配为止
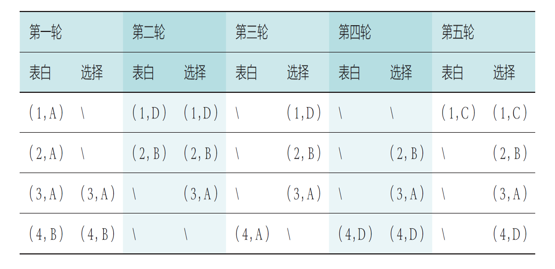
已知偏好序列:
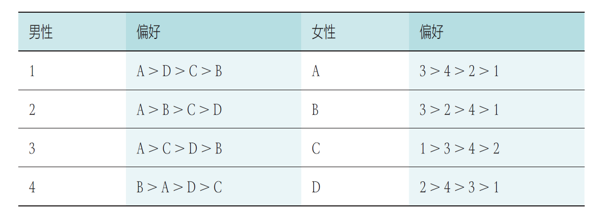
- 第一轮:4 名男性分别向自己最喜欢的女性告白,而收到 3 人告白的女性 A 选择了自己最喜欢的男性 3,另一个收到告白的女性 B 选择了男性 4
- 第二轮,尚未匹配的男性 1 和男性 2 继续向自己第二喜欢的对象告白,收到告白的女性 B 选择了自己更喜欢的男性 2 而放弃了男性 4
- 同理继续三轮告白和选择,所有人都找到了自己的伴侣,且所有匹配都是稳定的
- 可以看出,使用 G-S 算法得到了稳定匹配的结果
单边匹配问题: 最大交易圈 TTC
单边匹配问题:分配的对象都是不可分的标的物,他们只能属于一个所有者,且可以属于任何一个所有者
- 两种图节点:人节点和标的物节点,初始化可以随意分配
- 每个交易者连接一条指向他最喜欢的标的物的边,每一个标的物连接到其占有者或是具有高优先权的交易者
- 此时形成一张有向图,且必存在环,这种环被称为“交易圈”,
- 对于交易圈中的交易者,将每人指向结点所代表的标的物赋予交易者
- 交易者和标的物均离开市场
- 接着从剩余的交易者和标的物之间重复进行交易圈匹配,直到无法形成交易圈,算法停止
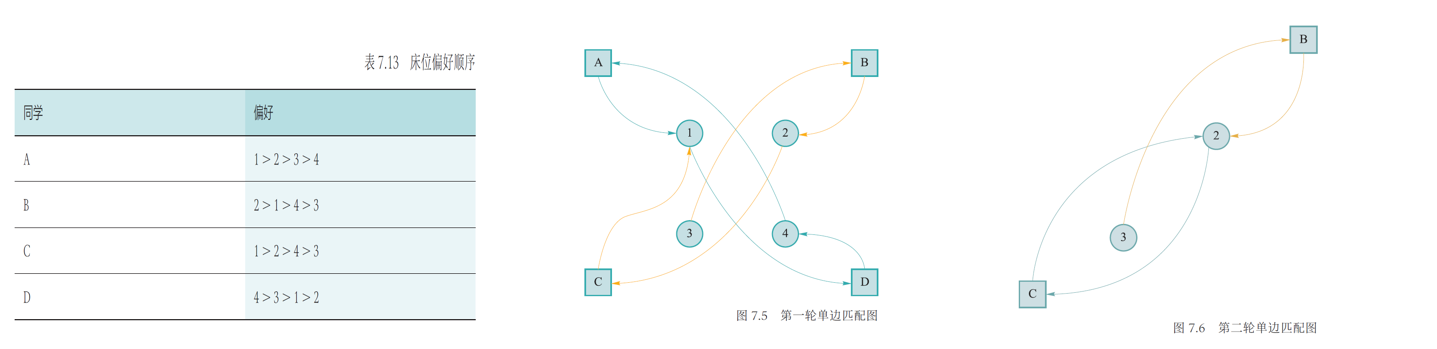
假设某寝室有 A、B、C、D 四位同学和 1、2、3、4 四个床位,当前给 A、B、C、D 四位同学随机分配 4、3、2、1 四个床位
在图 7.5 可以看出,A 和 D 之间构成一个交易圈,可达成交易,所以 A 得到床位 1,D 得到床位 4,之后将 A 和 D 以及 1 和 4 从匹配图中移除
从图 7.6 可以看出,B 和 C 都希望得到床位 2,无法再构成交易圈,但是由于 C 是床位的本身拥有者,所以 C 仍然得到床位 2,B 只能选择床位 3